해싱(hashing) 기본

해싱은 임의의 크기를 가진 데이터를 고정된 길이의 데이터로 변환시키는 것을 의미함.
변환시키는 함수가 해쉬함수(hash function)이다. 매핑하는 과정 자체를 해싱(hashing)이라 한다.

Direct Address Table (직접 주소 테이블)

직접 주소 테이블은 배열을 사용하여 레코드를 해당 키에 매핑 할 수있는 데이터 구조임.
직접 주소 테이블에서 키 값을 인덱스로 직접 사용하여 레코드가 배치된다. 즉, 빠른 검색, 삽입 및 삭제 작업이 용이하고 선형시간 O(1)이다.

똑같은 키 값이 존재하지 않는다고 가정하면, 해당 인덱스에 키 값을 저장하고 포인터로 데이터를 연결한다.
삭제 시에는 해당 키 위치에 NULL값을 넣어주면 된다. 탐색시에는 해당 키 값을 찾아가서 참조하면 된다.

다음 예제를 사용하여 개념을 이해할 수 있다.
최대 값에 1을 더한 크기의 배열 (0 기반 인덱스로 가정)을 생성 한 다음 값을 인덱스로 사용한다.
예를 들어, 다음 다이어그램에서 키 21은 인덱스로 직접 사용된다.

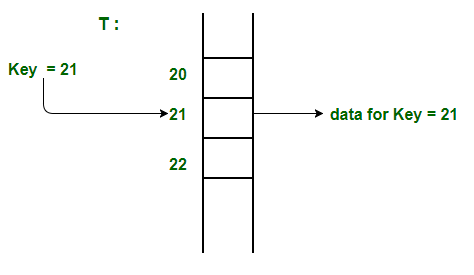
key값의 최대 크기만큼 배열이 할당된다.
크기는 매우 큰데, 저장하고자 하는 데이터가 적다면 공간을 낭비 할 수 있다.

Limitations:

Prior knowledge of maximum key value
Practically useful only if the maximum value is very less.
It causes wastage of memory space if there is a significant difference between total records and maximum value.
Hashing can overcome these limitations of direct address tables.

Hash Table

해시함수는 해쉬값의 개수보다 대개 많은 키값을 해쉬값으로 변환하기 때문에
해시함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시충돌(collision)이 발생하게 된다.

이름을 0~15 사이의 정수값으로 매핑하는 해시 함수의 예. “John Smith”와 “Sandra Dee”라는 두 키 사이에 충돌이 존재한다.

충돌 해결 방법

Chaining 방법과 Open Addressing 방법이 존재한다.

Chaining 방법 - 충돌을 허용하되 최소화하는 방법

한 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음으로써 모든 자료를 해시테이블에 담는 방식이다.
해당 버킷에 데이터가 이미 있다면 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식으로 구현(연결리스트)하기 때문에 체이닝이다.
유연하다는 장점을 가지나 메모리 문제를 야기할 수 있다.

때문에, 최초의 위치를 탐색하는 해쉬 과정은 제외하고 모든 탐색, 삽입, 삭제 과정은 연결리스트와 유사한 방식으로 진행된다.

Open Addressing(개방 주소법) 방법

key값을 테이블에 저장하는 직접 주소 테이블(Direct Address Table)과 다르게 Open Addressing는 모든 데이터(key + 데이터)를 테이블에 저장하는 방법이다.

체이닝의 경우 버켓이 꽉 차더라도 연결리스트로 계속 늘려가기에, 데이터의 주소값은 바뀌지 않는다.(Closed Addressing) 하지만 개방 주소법의 경우에는 다르다. 해시 충돌이 일어나면 다른 버켓에 데이터를 삽입하는 방식을 개방 주소법이라고 한다. 개방 주소법은 대표적으로 3가지가 있다.

선형 탐색(Linear Probing): 해시충돌 시 다음 버켓, 혹은 몇 개를 건너뛰어 데이터를 삽입한다.  
제곱 탐색(Quadratic Probing): 해시충돌 시 제곱만큼 건너뛴 버켓에 데이터를 삽입(1,4,9,16..)  
이중 해시(Double Hashing): 해시충돌 시 다른 해시함수를 한 번 더 적용한 결과를 이용함.  

개방 주소법의 장점은 아래와 같다.

체이닝처럼 포인터가 필요없고, 지정한 메모리 외 추가적인 저장공간도 필요없다.
삽입,삭제시 오버헤드가 적다.
저장할 데이터가 적을 때 더 유리하다.

참고자료